<- Tillbaks

Datastrukturer och Algoritmer

Innehållsförteckning

Sök algoritmer

Linjär sökning

Kollar varje element i en sekvensiell ordning
Tidskomplexitet (Medelvärde): O(n)
Bästa fall: O(1)
Sämsta fall: O(n)

Binär sökning

Kräver att listan är sorterad
Delar listan i två delar och kollar om elementet finns i den vänstra eller högra delen
Tidskomplexitet (Medelvärde): O(log n)
Bästa fall: O(1)
Sämsta fall: O(log n)

Sorteringsalgoritmer

Bubble sort

Jämför två intilliggande (adjacent) element och byter plats om de är i fel ordning
Tidskomplexitet (Medelvärde): O(n^2)
Bästa fall: O(n)
Sämsta fall: O(n^2)
Utrymme: O(1)

Bubble Sort


void bubbleSort(int arr[], int n)
{
    for (int i = 0; i < n - 1; i++) {
        for (int j = 0; j < n - i - 1; j++) {
            if (arr[j] > arr[j + 1]) {
                // Swap arr[j] and arr[j+1]
                int temp = arr[j];
                arr[j] = arr[j + 1];
                arr[j + 1] = temp;
            }
        }
    }
}

Selection sort

Hittar det minsta elementet i listan och byter plats med det första elementet
Tidskomplexitet (Medelvärde): O(n^2)
Bästa fall: O(n^2)
Sämsta fall: O(n^2)
Utrymme: O(1)

Selection sort


void selectionSort(int arr[], int n)
{
    for (int i = 0; i < n - 1; i++) {
        int indexOfMinimum = i;
        for (int j = i + 1; j < n; j++)
            if (arr[j] < arr[indexOfMinimum])
                indexOfMinimum = j;

        // Swap the found minimum element with the first element
        if (indexOfMinimum != i) {
            int temp = arr[indexOfMinimum];
            arr[indexOfMinimum] = arr[i];
            arr[i] = temp;
        }
    }
}

Insertion sort

Delar listan i en sorterad och en osorterad del. Tar ett element från den osorterade delen och placerar det i den sorterade delen
Tidskomplexitet (Medelvärde): O(n^2)
Bästa fall: O(n)
Sämsta fall: O(n^2)
Utrymme: O(1)

Insertion sort


void insertionSort(int arr[], int n)
{
    for (int i = 1; i < n; i++) {
        int key = arr[i];
        int j = i - 1;

        /* Move elements that are greater than key
           to one position ahead of their current position */
        while (j >= 0 && arr[j] > key) {
            arr[j + 1] = arr[j];
            j--;
        }
        arr[j + 1] = key;
    }
}

Merge sort

Delar listan i två delar och sorterar varje del separat. Sedan kombineras de sorterade delarna
Tidskomplexitet (Medelvärde): O(n log n)
Bästa fall: O(n log n)
Sämsta fall: O(n log n)
Utrymme: O(n)

Merge sort


void mergeSort(int array[], int n)
{
    if (n < 2)
        return; // Base case, can't split any more
    int mid = n / 2;
    int left[mid];
    int right[n-mid];

    for (int i = 0; i < mid; i++)
        left[i] = array[i];

    for (int i = mid; i < n; i++)
        right[i - mid] = array[i];

    mergeSort(left, mid);
    mergeSort(right, n - mid);

    merge(array, left, right, mid, n - mid);
}

Quick sort

Väljer ett pivot element och delar listan i två delar. Elementen mindre än pivoten placeras till vänster och elementen större till höger
Tidskomplexitet (Medelvärde): O(n log n)
Bästa fall: O(n log n)
Sämsta fall: O(n^2)
Utrymme: O(log n)

Quick sort

Structs & Typedef

Structs används för att skapa egna datatyper
Typedef för att skapa egna datatyper
Structs kan innehålla andra structs
Structs kan innehålla variabler, räckor och pekare


// Typedef och struct
typedef struct {
 int day;
 int month;
 int year;
} Date;

// Struct som innehpller struct
typedef struct {
 char name[10];
 Date date;
} Object;

// Variabl med struct
Date d1 = { 30, 10, 2024 };

// Ändra värden i struct
d1.month++;

// Array med struct
Date dateArray[100];

// Fylla array med struct
memset(dateArray, 0, sizeof(Date) * 100);

// Ändra värden i array med struct
dateArray[0] = (Date){30, 10, 2024};

// Ändra värden i array med struct
dateArray[0].year = 2024;

Rekursion

En funktion som anropar sig själv
Används för att lösa problem som kan delas upp i mindre delproblem
Kan vara svårt att felsöka
Kan leda till stackoverflow om det finns för många anrop
Kan vara långsamt


/*
 * n! = n * (n-1) * (n-2) * ... * 1
 * 5! = 5 * 4 * 3 * 2 * 1 = 120
*/
int factorial(int n) {
 if (n == 0) {
  return 1;
 }
 return n * factorial(n - 1);
}

/*
 * Fibonacci
 * 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, ...
*/
int fibonacci(int n) {
 if (n == 0) {
  return 0;
 }
 if (n == 1) {
  return 1;
 }
 return fibonacci(n - 1) + fibonacci(n - 2);
}

/*
 * Summan av alla tal från 1 till n
 * 1 + 2 + 3 + 4 + 5 + ... + n
*/
int sum(int n) {
 if (n == 0) {
  return 0;
 }
 return n + sum(n - 1);
}

/*
 * Binär sökning
*/
int binarySearch(int arr[], int n, int e)
{
    return binarySearchRecursive(arr, 0, n - 1, e);
}

int binarySearchRecursive(int array[], int lowIndex, int highIndex, int e)
{
    if (highIndex >= lowIndex) {
        int midIndex = lowIndex + (highIndex - lowIndex) / 2;
        if (array[midIndex] == e)
            return midIndex; // Base case 1 - element found
        if (array[midIndex] > e)
            return binarySearchRecursive(array, lowIndex, midIndex - 1, e);
	  else
            return binarySearchRecursive(array, midIndex + 1, highIndex, e);
    }
    return -1; // Base case 2 - element not found
}

Pekare (Pointers)

En pekare är en variabel som innehåller en adress till en annan variabel
Används för att referera till en variabel
Används för att skicka pekare till funktioner
Används för att allokera och frigöra minne


// Deklartion av pekare
int *pointer;

// Initialisering av pekare
int value = 10;
int *pointer = &value;

// Dereferensering av pekare
int value = 10;
int *pointer = &value;
int dereferencedValue = *pointer;
printf("%d\n", *pointer); // 10

// Två pekare till samma variabel
char value = 'A';
char *pointer1 = &value;
char *pointer2 = &value;

// Null pekare
int *pointer = NULL;

// Pekare som funktionsparametrar
void foo(int *pointer) {
 *pointer = 20;
}

int value = 10;
foo(&value);
printf("%d\n", value); // 20

// Pekare och räckor
int values[5] = {1, 2, 3, 4, 5};
int *pointer = values;
printf("%d\n", *pointer); // 1
printf("%d\n", *(pointer + 1)); // 2

// Pekare och strukturer

typedef struct {
 int day;
 int month;
 int year;
} Date;

Date date = { 30, 10, 2024 };

Date *pointer = &date;

printf("%d\n", pointer->day); // 30
printf("%d\n", (*pointer).month); // 10

// Funktioner som returnerar pekare

Date *getDate() {
 Date date = { 30, 10, 2024 };
 return &date;
}

Dynamisk minnesallokering

Används för att allokera minne under körningstid


// Allokera minne
int size = 10;
int *arrayPointer = malloc(sizeof(int) * size);

// Omallokera minne
arrayPointer = realloc(arrayPointer, sizeof(int) * (size*2));

/*
 * Minnesläcka kan hända om man använder malloc flera gånger på samma pekare
*/

// Frigör minne
free(arrayPointer);

Länkade listor

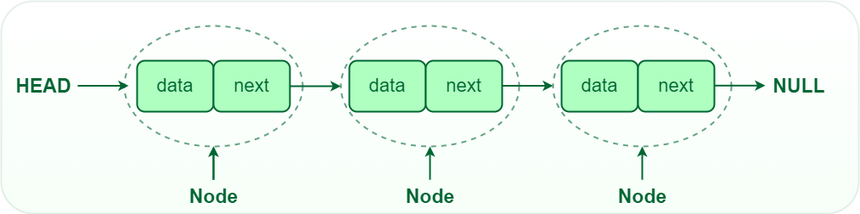
En länkad lista består av noder som innehåller data och en pekare till nästa nod
En dubbel länkad lista innehåller även en pekare till föregående nod
En cirkulär länkad lista har en pekare från sista noden till första noden
En länkad lista behöver alltid en head nod
Tidskomplexitet (Medelvärde): O(n)


typedef struct {
 int data;
 char data2;
} Data;

// Enkel länkad lista
typedef struct {
 Data data;
 // Pekare till nästa nod
 struct Node *next;
} Node;

// Skapa en nod
Node *createNode(int data) {
 Node *node = malloc(sizeof(Node));
 if (node == NULL) {
  return NULL;
 }
 node->data = data;
 node->next = NULL;
 return node;
}

Data data = { 10, 'A' };

// Skapa en nod. Länkad lista behöver alltid en head nod
Node *head = createNode(&data);

Stackar och köer

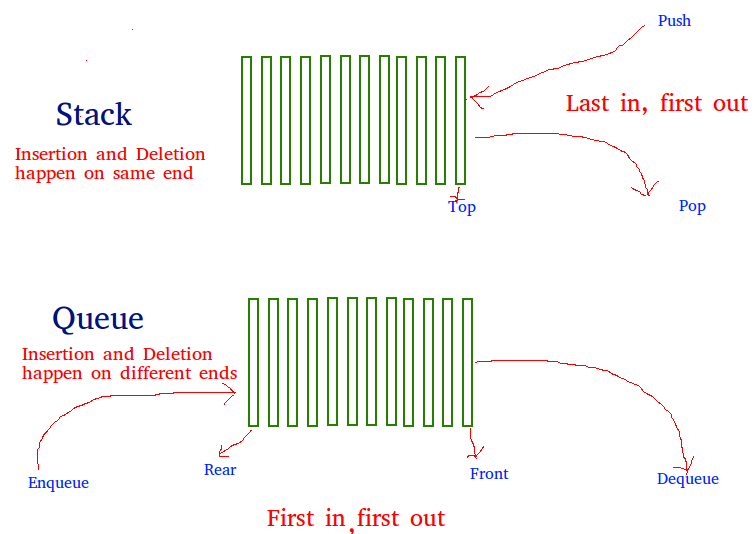
Stack (LIFO - Last In First Out) Som betyder att det sista elementet som sätts in är det första som tas ut
Kö / Queue (FIFO - First In First Out) Som betyder att det första elementet som sätts in är det första som tas ut


typedef struct {
 int data;
 char data2;
} Data;

// Stack (LIFO)

typedef struct {
 Data data;
 struct Stack *next;
} Stack;

// Koe (FIFO)

typedef struct {
 Data data;
 Queue *next;
} Queue;

Binära träd

Ett binärt träd är en datastruktur som består av noder som innehåller data och pekare till vänster och höger nod
Tidskomplexitet (Medelvärde): O(n log n)


// Binärt träd nod
typedef struct {
 int data;
 struct Node *left;
 struct Node *right;
} Node;


// Skapa en nod
Node *createNode(int data) {
 Node *node = malloc(sizeof(Node));
 if (node == NULL) {
  return NULL;
 }
 node->data = data;
 node->left = NULL;
 node->right = NULL;
 return node;
}

// Sätt in en nod i trädet
void insert(Node **root, int data) {
 if (*root == NULL) {
  *root = createNode(data);
  return;
 }
 if (data < (*root)->data) {
  insert(&(*root)->left, data);
 } else {
  insert(&(*root)->right, data);
 }
}

Hash tabeller

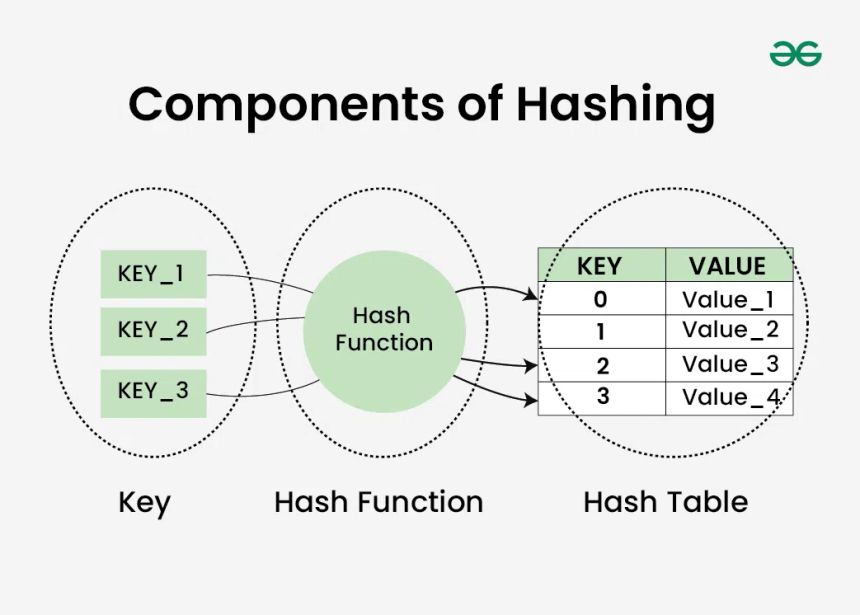
En hash tabell är en datastruktur som används för att lagra nyckel-värde par
En hash funktion används för att beräkna index för varje nyckel
En hash tabell används för att hitta data med hjalp av nyckel
Kollisioner kan lösas med hjälp av linjär sökning eller länkad lista
Tidskomplexitet (Medelvärde): O(1)


// Hash tabell element
typedef struct {
	int key;
 	int data;
} HashElement;

// Hash tabell
#define TABLE_SIZE 100
HashElement *hashTable[TABLE_SIZE];

// Hash funktion
int hashFunction(int key) {
	return key % TABLE_SIZE;
}

// Sätt in element i hash tabell
void insert(int key, int data) {
	int index = hashFunction(key);
	hashTable[index] = malloc(sizeof(HashElement));
	hashTable[index]->key = key;
	hashTable[index]->data = data;
}

// Sök efter element i hash tabell
HashElement *search(int key) {
	int index = hashFunction(key);
	return hashTable[index];
}